ReLU、Dropout、mini-batch、BN、L1/L2、finetune等等
ReLU
关于激活函数的作用以及Sigmoid、tanh的性质这里不再赘述
ReLU全称是Rectified Liner Uints,修正线性单元,又称线性整流函数,是一种稀疏激活函数,于2010~2011年提出,其具体形式为y=max(0,x)。
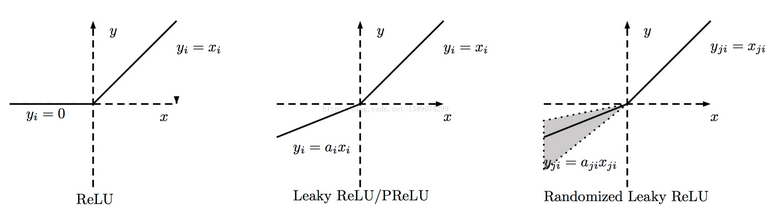
ReLU优点
1、单侧抑制;
2、相对宽阔的兴奋边界;
3、稀疏激活性
4、解决梯度消失问题
标准的sigmoid函数输出不具备稀疏性,需要用一些惩罚因子来训练出一大堆接近0的冗余数据来,从而产生稀疏数据,例如L1、L1/L2或Student-t作惩罚因子。
ReLU是线性修正,它的作用是如果计算出的值小于0,就让它等于0,否则保持原来的值不变。这是一种简单粗暴地强制某些数据为0的方法,然而经实践证明,训练后的网络完全具备适度的稀疏性。
ReLu的使用,使得网络可以自行引入稀疏性,同时大大地提高了训练速度。
稀疏性的优势
这里有必要介绍一下稀疏性的优势
1.信息解离。 原始输入数据往往缠绕着高密度特征,特征之间相互耦合,表现出强烈的非线性特征.传统学习算法往往是采用高维映射等手段进行信息解理,但是往往难以很好的进行解耦。若能通过手段将这些特征转换为稀疏特征,则特征之间耦合更小,特征鲁棒性更强。
2.线性可分。稀疏性特征之间耦合小,具有更好的线性可分性,使用简单的线性分类器即可有好的效果
3.保留了原始稠密特征的性能。原始数据所表现出来的稠密特性, 而稀疏性是从稠密特征中解耦得来,在线性可分的同时也保留了原始稠密特征的性能,具有很大的潜力.
稀疏激活函数的优势
若激活函数具有稀疏性,则可以更好的从有效的数据维度上,学习到相对稀疏的特征,起到特征自动解耦的作用。
1.非饱和线性端。相比于BP网络、SVM等分类器。采用线性激活函数,网络更快更高效。??此处还需调研一下
2.解决梯度消失问题
3.目前的DL架构中,合理的稀疏性比率为70~80%,否则屏蔽特征多过,容易出现欠拟合现象.
梯度消失问题Gradient vanishing
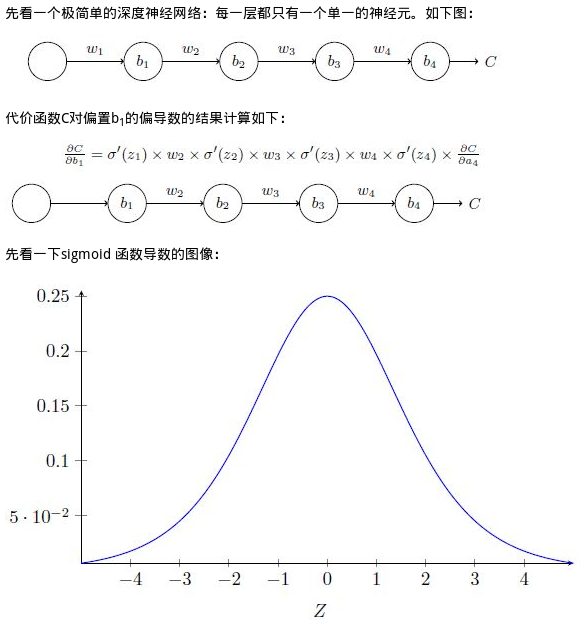
该导数在σ′(0) = 1/4时达到最高。现在,如果我们使用标准方法来初始化网络中的权重,那么会使用一个均值为0 标准差为1 的高斯分布。因此所有的权重通常会满足|wj|<1。从而有wjσ′(zj) < 1/4。
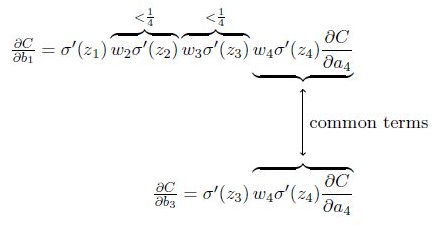
ReLU的缺陷
训练过程该函数不适应较大梯度输入,因为在参数更新以后,ReLU的神经元不会再有激活的功能,导致梯度永远都是零。
另外,当学习率过大的时候也会存在这种问题.
如W’=W - lr*delta(w), 这里delta(w)指的是反向传播的梯度, lr是学习率, 当delta(w)或者lr过大的时候, w’可能变为负值。在此后计算梯度的时候delta(w)将始终为0
为了针对以上的缺点,又出现Leaky-ReLU、P-ReLU、R-ReLU三种拓展激活函数。
Dropout
我们知道过拟合是训练神经网络的大忌,通常解决过拟合问题有四种途径,
1.提前终止(当验证集上的效果变差的时候)
2.L1和L2正则化加权
3.soft weight sharing
4.Dropout
Dropout的基本思想是引入Bernouli随机数,概率p舍弃神经元并让其它神经元以概率q=1-p保留,舍去的神经元的输出都被设置为零。
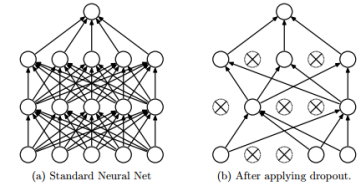
没有Dropout的神经网络
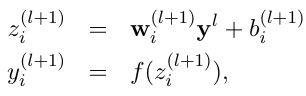
有Dropout的神经网络
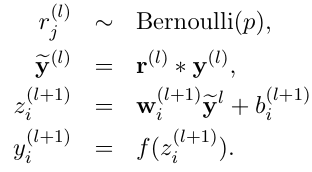
Dropout保证样本均值不会发生变化

当前Dropout被大量利用于全连接网络,而且参数一般设置为0.5或者0.3,而在卷积隐藏层由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因,Dropout策略在卷积隐藏层中使用较少。
Gradient Descent
Batch Gradient Descent(BGD)
批梯度下降法(Batch Gradient Descent)针对的是整个数据集,通过对所有的样本的计算来求解梯度的方向
每迭代一步,都要用到训练集所有的数据,如果样本数目很大,迭代速度会极慢。
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
Stochastic Gradient Descent(SGD)
随机梯度下降法,每次迭代只使用一个训练样本,每次只使用一个样本迭代,若遇上噪声则容易陷入局部最优解。
Mini-batch Gradient Descent
这是介于BSD和SGD之间的一种优化算法。每次选取一定量的训练样本进行迭代。
由于每次更新用了多个样本来计算loss,就使得loss的计算和参数的更新更加具有代表性。不像原始SGD很容易被某一个样本给带偏 。loss的下降更加稳定,同时小批量的计算,也减少了计算资源的占用。
该方法速度比BSD快,比SGD慢;精度比BSD低,比SGD高.
带Mini-batch的SGD
1.选择n个训练样本(n<m,m为总训练集样本数)
2.在这n个样本中进行n次迭代,每次使用1个样本
3.对n次迭代得出的n个gradient进行加权平均再并求和,作为这一次mini-batch下降梯度
4.不断在训练集中重复以上步骤,直到收敛。
对比分析

如下图,左边是BSD的梯度下降效果,由于是对整个数据集迭代一次计算一次损失,因此呈现平稳下降的趋势。右边是Mini-batch的梯度下降效果,以看到它是上下波动的,成本函数的值有时高有时低,但总体还是呈现下降的趋势。
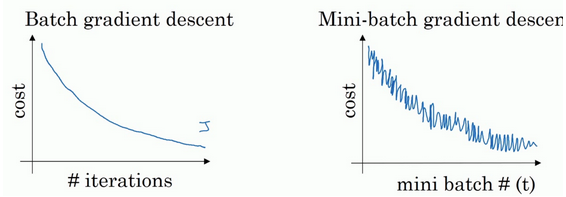
把上面的图看做是梯度下降空间。蓝色的部分是full batch的而上面是mini batch。mini batch不是每次迭代损失函数都会减少,看上去好像走了很多弯路,不过整体还是朝着最优解迭代的。而且由于mini batch一个epoch就走了几千步,而full batch一个epoch只有一步,所以虽然mini batch走了弯路但还是会快很多.
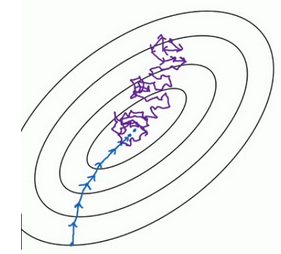
Batch Normalization
起因
CNN网络在训练的过程中,前一层的参数变化影响着后面层的变化(因为前面层的输出是后面的输入),而且这种影响会随着网络深度的增加而不断放大。
在CNN训练时,绝大多数都采用mini-batch使用随机梯度下降算法进行训练,那么随着输入数据的不断变化,以及网络中参数不断调整,网络的各层输入数据的分布则会不断变化,那么各层在训练的过程中就需要不断的改变以适应这种新的数据分布,从而造成网络训练困难,难以拟合的问题。
Batch Normalization是2015年Google研究员在论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》一文中提出的,同时也将BN应用到了2014年的GoogLeNet上,也就是Inception-v2。
BN算法的几大优势
1.无论学习率大小如何,都能很快收敛
2.无需再使用Dropout
3.可以把训练数据彻底打乱
4.无需使用局部响应归一化层
5.有效避免梯度消失与梯度爆炸,同时作为一种正则化技术也提高了泛化能力
BN算法细节
首先,BN算法在每一次iteration中的每一层输入都进行了归一化,将输入数据的分布归一化为均值为0,方差为1的分布
但是这种做法有一个致命的缺点,尽管这样把每层的数据分布都固定了,但是这种分布不一定是前面一层的要学习到的数据分布,这样强行归一化就会破坏掉刚刚学习到的特征.
于是算法使用了变换重构,引入了可学习参数γ、β,这就是算法关键之处
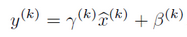
每一个神经元xk都会有一对这样的参数γ、β。这样其实当:
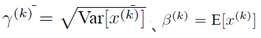
是可以恢复出原始的某一层所学到的特征的。因此我们引入了这个可学习重构参数γ、β,让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式就是
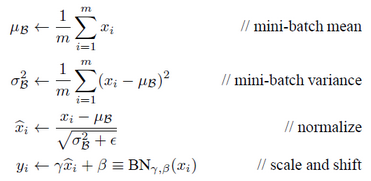
上面的公式中m指的是mini-batch size
L1/L2正则化
机器学习中几乎都可以看到损失函数后面会添加一个额外项,常用的额外项一般有两种,称作L1正则化和L2正则化,或者L1范数和L2范数,目的主要是防止过拟合,提高泛化能力。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓惩罚是指对损失函数中的某些参数做一些限制。这里在之前关于过拟合与欠拟合的博客中有提到。
L2 regularization
L2正则化就是在代价函数后面再加上一个正则化项
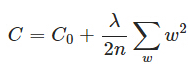
C0代表原始的代价函数,后面那一项就是L2正则化项。即全部参数w的平方的和,除以训练集的样本大小n。
λ就是正则项系数,权衡正则项与C0项的比重。另外系数1/2主要是为了后面求导的结果方便,后面那一项求导会产生一个2,与1/2相乘刚好凑整。
L2正则化项是怎么避免overfitting的,先求导
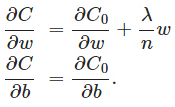
能够发现L2正则化项对b的更新没有影响,可是对于w的更新有影响:
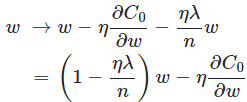
在不使用L2正则化时。求导结果中w前系数为1,如今w前面系数为 1−ηλ/n ,由于η、λ、n都是正的。所以 1−ηλ/n小于1,它的效果是减小w。这也就是权重衰减(weight decay)的由来。
当然考虑到后面的导数项,w终于的值可能增大也可能减小。
另外。须要提一下,对于基于mini-batch的随机梯度下降,w和b更新的公式跟上面给出的有点不同
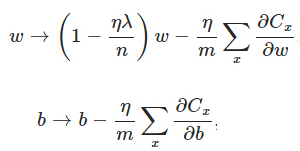
L2正则化能够让w有变小的趋势。现在解释一下w变小为什么能够防止过拟合。
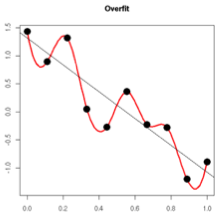
过拟合的时候,拟合函数的系数往往非常大。例如下图,过拟合就是拟合函数须要顾忌每个点。在某些非常小的区间里,函数值的变化非常剧烈。
这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以仅仅有系数足够大,才干保证导数值非常大。
L1 regularization
在原始的代价函数后面加上一个L1正则化项。即全部权重w的绝对值的和,乘以λ/n
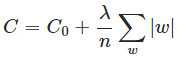
先计算导数
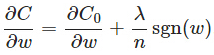
上式中sgn(w)表示w的符号。那么权重w的更新规则为
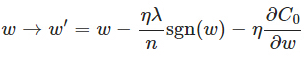
比原始的更新规则多出了η λ sgn(w)/n这一项。
当w为正时,更新后的w变小;当w为负时。更新后的w变大。
因此它的效果就是让w往0靠,使网络中的权重尽可能为0,也就相当于减小了网络复杂度,防止过拟合。
L1与L2的区别
L1可以让一部分特征系数缩小到0,可以得到稀疏的权值,从而间接实现特征选择,适合特征之间有关联的情况。
L2让所有特征系数都缩小,但是不会减为0,可以得到平滑的权值,使得优化求解稳定快速,适用于特征之间没有关联的情况。
finetune
所谓finetune就是用别人训练好的模型,加上我们自己的数据,来训练新的模型。finetune相当于使用别人的模型的前几层,来提取浅层特征,然后在最后再落入我们自己的分类中。
finetune的好处在于不用完全重新训练模型,从而提高效率,因为一般新训练模型准确率都会从很低的值开始慢慢上升,但是finetune能够让我们在比较少的迭代次数之后得到一个比较好的效果。在数据量不是很大的情况下,finetune会是一个比较好的选择。但是如果希望定义自己的网络结构的话,就需要从头开始。
假设网络结构不改变,finetune的简单步骤如下:
1.依然是准备好我们的训练数据和测试数据
2.计算数据集的均值文件
使用caffe下的convert_imageset工具
3.修改网络最后一层的名字、输出类别数,并且需要加快最后一层的参数学习速率
首先修改名字,这样预训练模型赋值的时候这里就会因为名字不匹配从而重新训练,也就达成了我们适应新任务的目的。
调整学习速率,因为最后一层是重新学习,因此需要有更快的学习速率相比较其他层,因此我们将,weight和bias的学习速率加快10倍(lr_mult)。
4.调整Solver的配置参数,通常学习速率和步长,迭代次数都要适当减少
5.启动训练,并且需要加载pretrained模型的参数
迁移学习Transfer Learning
迁移学习(Transfer learning) 顾名思义就是就是把已学训练好的模型参数迁移到新的模型来帮助新模型训练。考虑到大部分数据或任务是存在相关性的,所以通过迁移学习我们可以将已经学到的模型参数(也可理解为模型学到的知识)通过某种方式来分享给新模型,从而加快并优化模型的学习效率,不用像大多数网络那样从零学习
迁移学习只是一种思想,Transfer Learning关心的问题是:什么是“知识”以及如何更好地运用之前得到的“知识”。这可以有很多方法和手段,finetune只是其中的一种手段。
参考文献
【1】[DeepLearning学习笔记之ReLU函数]https://blog.csdn.net/l349074299/article/details/72680078
【2】[ReLU函数简介]https://blog.csdn.net/u012905422/article/details/52601022
【3】[消失的梯度问题]https://www.cnblogs.com/tsiangleo/p/6151560.html
【4】[理解dropout]https://blog.csdn.net/stdcoutzyx/article/details/49022443
【5】[mini-batch 梯度下降]https://blog.csdn.net/kebu12345678/article/details/54917600
【6】[深度学习基础 (五)–超参数:mini batch]https://testerhome.com/topics/10877
【7】[Batch Normalization 学习笔记]https://blog.csdn.net/leayc/article/details/77645877
【8】[正则化方法:L1和L2 regularization、数据集扩增、dropout]https://www.cnblogs.com/yxwkf/p/5268577.html
【9】[Caffe 使用记录(三)finetune]https://www.cnblogs.com/xuanyuyt/p/6062204.html
【10】[什么是迁移学习]https://www.zhihu.com/question/41979241/answer/123545914