分类算法汇总(二)

发表于 | 更新于 | 分类于 | 阅读次数：
本文字数： 6.5k | 阅读时长 ≈ 6 分钟

bagging,随机森林,Adaboost

集成学习通过将多个学习器进行整合,常可获得比单一学习器显著优越的泛化性能,这对弱分类器尤为明显。

bagging

自举汇聚法(booststrap aggregating)，也称为bagging方法，是在从原始数据集选择S次后得到S个新数据集的一种技术。
新数据集与原数据集大小相等，每个数据集都是通过在原始数据集中随机选择一个样本来进行替换得到的(这里也可以通过放回取样，新数据集中的每个样本都是从原数据集中有放回地随机抽样得到)
在S个数据集建好之后，将某个学习算法分别作用于每个数据集，就得到了S个分类器。
然后应用这S个分类器对新的数据进行分类，选择分类器投票结果最多的类别作为最后的分类结果。
对于回归任务，采用的是简单平均的方法计算最后的结果。

随机森林

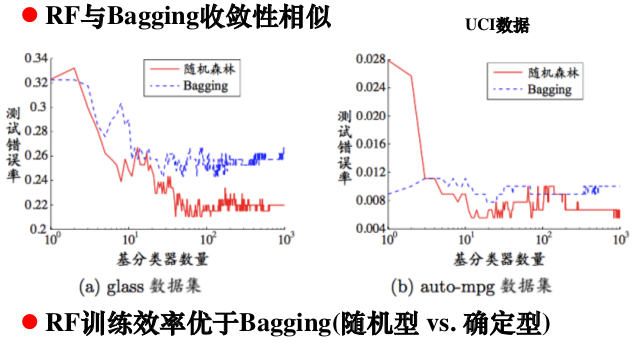
随机森林(Random Forest,RF)是bagging方法的一种扩展变体，以决策树为基学习器，训练过程引入随机属性选择

基本思想

对于基决策树的每个结点，先从该结点的(d个)属性集合中随机选择一个包含k个属性的子集，再从这个子集选择一个最优属性用于划分，一般情况下推荐k=logd

1.如果训练集大小为N，对于每棵树而言，随机且有放回地从训练集中的抽取N个训练样本，作为该树的训练集；
2.随机地从d个特征中选取k个特征子集，每次树进行分裂时，从这k个特征中选择最优的；
3.每棵树都尽最大程度的生长，并且没有剪枝过程。

"da"
"da"

算法特点

1.基学习器多样性通过样本扰动和属性扰动实现
2.性能强大,被誉为“代表集成学习技术水平的方法”
3.算法简单、容易实现、计算开销小

Adaboost

Adaboost是Adaptive boosting的缩写，它的自适应在于：前一个基本分类器被错误分类的样本的权值会增大，而正确分类的样本的权值会减小，并再次用来训练下一个基本分类器。同时，在每一轮迭代中，加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器。

算法流程

Adaboost一般使用单层决策树作为其弱分类器。单层决策树是决策树的最简化版本，只有一个决策点

"da"

实例代码

先建立一个简单的数据集，并将其转为我们想要的数据格式，代码如下

1
2
3
4
5
6
7
8
9
 #获取数据集
def loadSimpData():
    dataMat=matrix([[1.0,2.1],
        [2.0,1.1],
        [1.3,1.0],
        [1.0,1.0],
        [2.0,1.0]])
    classLabels=[1.0,1.0,-1.0,-1.0,1.0]
return dataMat,classLabels

接下来，我们就要通过上述数据集来寻找最佳的单层决策树，最佳单层决策树是具有最低分类错误率的单层决策树，伪代码如下：

1
2
3
4
5
6
7
8
9
10
#构建单层分类器
#单层分类器是基于最小加权分类错误率的树桩
#伪代码
#将最小错误率minError设为+∞
#对数据集中的每个特征(第一层特征)：
   #对每个步长(第二层特征)：
       #对每个不等号(第三层特征)：
           #建立一颗单层决策树并利用加权数据集对它进行测试
           #如果错误率低于minError，则将当前单层决策树设为最佳单层决策树
#返回最佳单层决策树

接下来看单层决策树的生成函数代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
 #单层决策树的阈值过滤函数
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):
    #对数据集每一列的各个特征进行阈值过滤
    retArray=ones((shape(dataMatrix)[0],1))
    #阈值的模式，将小于某一阈值的特征归类为-1
    if threshIneq=='lt':
        retArray[dataMatrix[:,dimen]<=threshVal]=-1.0
    #将大于某一阈值的特征归类为-1
    else:
        retArray[dataMatrix[:,dimen]>threshVal]=-1.0
        
def buildStump(dataArr,classLabels,D):
 #将数据集和标签列表转为矩阵形式
    dataMatrix=mat(dataArr);labelMat=mat(classLabels).T
    m,n=shape(dataMatrix)
    #步长或区间总数 最优决策树信息 最优单层决策树预测结果
    numSteps=10.0;bestStump={};bestClasEst=mat(zeros((m,1)))
    #最小错误率初始化为+∞
    minError=inf
    #遍历每一列的特征值
    for i in range(n):
        #找出列中特征值的最小值和最大值
        rangeMin=dataMatrix[:,i].min();rangeMax=dataMatrix[:,i].max()
        #求取步长大小或者说区间间隔
        stepSize=(rangeMax-rangeMin)/numSteps
        #遍历各个步长区间
        for j in range(-1,int(numSteps)+1):
            #两种阈值过滤模式
            for inequal in ['lt','gt']:
            #阈值计算公式：最小值+j(-1<=j<=numSteps+1)*步长
            threshVal=(rangeMin+float(j)*stepSize)
            #选定阈值后，调用阈值过滤函数分类预测
            predictedVals=\
                stumpClassify(dataMatrix,i,threshVal,'inequal')
            #初始化错误向量
            errArr=mat(ones((m,1)))
            #将错误向量中分类正确项置0
            errArr[predictedVals==labelMat]=0
            #计算"加权"的错误率
            weigthedError=D.T*errArr
            #打印相关信息，可省略
            #print("split: dim %d, thresh %.2f,thresh inequal:\
            #    %s, the weighted error is %.3f",
            #    %(i,threshVal,inequal,weigthedError))
            #如果当前错误率小于当前最小错误率，将当前错误率作为最小错误率
            #存储相关信息
            if weigthedError<minError:
                minError=weigthedError
                bestClasEst=predictedVals.copy()
                bestStump['dim']=i
                bestStump['thresh']='threshVal'
                bestStump['ineq']=inequal
    #返回最佳单层决策树相关信息的字典，最小错误率，决策树预测输出结果
    return bestStump,minError,bestClasEst

上面已经构建好了基于加权输入值进行决策的单层分类器，那么就已经有了实现一个完整AdaBoost算法所需要的所有信息了。下面先看一下整个AdaBoost的伪代码实现

1
2
3
4
5
6
7
8
9
#完整AdaBoost算法实现
#算法实现伪代码
#对每次迭代：
   #利用buildStump()函数找到最佳的单层决策树
   #将最佳单层决策树加入到单层决策树数组
   #计算alpha
   #计算新的权重向量D
   #更新累计类别估计值
   #如果错误率为等于0.0，退出循环

具体实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
 #adaBoost算法
 #@dataArr：数据矩阵
 #@classLabels:标签向量
 #@numIt:迭代次数    
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
    #弱分类器相关信息列表
    weakClassArr=[]
    #获取数据集行数
    m=shape(dataArr)[0]
    #初始化权重向量的每一项值相等
    D=mat(ones((m,1))/m)
    #累计估计值向量
    aggClassEst=mat((m,1))
    #循环迭代次数
    for i in range(numIt):
        #根据当前数据集，标签及权重建立最佳单层决策树
        bestStump,error,classEst=buildStump(dataArr,classLabels,D)
        #打印权重向量
        print("D:",D.T)
        #求单层决策树的系数alpha
        alpha=float(0.5*log((1.0-error)/(max(error,1e-16))))
        #存储决策树的系数alpha到字典
        bestStump['alpha']=alpha
        #将该决策树存入列表
        weakClassArr.append(bestStump)
        #打印决策树的预测结果
        print("classEst:",classEst.T)
        #预测正确为exp(-alpha),预测错误为exp(alpha)
        #即增大分类错误样本的权重，减少分类正确的数据点权重
        expon=multiply(-1*alpha*mat(classLabels).T,classEst)
        #更新权值向量
        D=multiply(D,exp(expon))
        D=D/D.sum()
        #累加当前单层决策树的加权预测值
        aggClassEst+=alpha*classEst
        print("aggClassEst",aggClassEst.T)
        #求出分类错的样本个数
        aggErrors=multiply(sign(aggClassEst)!=\
                    mat(classLabels).T,ones((m,1)))
        #计算错误率
        errorRate=aggErrors.sum()/m
        print("total error:",errorRate,"\n")
        #错误率为0.0退出循环
        if errorRate==0.0:break
    #返回弱分类器的组合列表
    return weakClassArr

测试算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
 #测试adaBoost，adaBoost分类函数
 #@datToClass:测试数据点
 #@classifierArr：构建好的最终分类器
def adaClassify(datToClass,classifierArr):
    #构建数据向量或矩阵
    dataMatrix=mat(datToClass)
    #获取矩阵行数
    m=shape(dataMatrix)[0]
    #初始化最终分类器
    aggClassEst=mat(zeros((m,1)))
    #遍历分类器列表中的每一个弱分类器
    for i in range(len(classifierArr)):
        #每一个弱分类器对测试数据进行预测分类
        classEst=stumpClassify(dataMat,classifierArr[i]['dim'],\
                                classifierArr[i]['thresh'],
                                classifierArr[i]['ineq'])
        #对各个分类器的预测结果进行加权累加
        aggClassEst+=classifierArr[i]['alpha']*classEst
        print('aggClassEst',aggClassEst)
    #通过sign函数根据结果大于或小于0预测出+1或-1
    return sign(aggClassEst)

优缺点

AdaBoost在每一轮的迭代过程中都会基于弱分类器的加权错误率，更新权重向量，从而进行下一次迭代。并且会在每一轮迭代中计算出该弱分类器的系数，该系数的大小将决定该弱分类器在最终预测分类中的重要程度。这两点的结合是adaBoost算法的优势所在。

优点
1.Adaboost提供一种框架，在框架内可以使用各种方法构建子分类器。可以使用简单的弱分类器，不用对特征进行筛选，也不存在过拟合的现象。泛化错误率低，容易实现，可以应用在大部分分类器上，无参数调整
2.Adaboost算法不需要弱分类器的先验知识，最后得到的强分类器的分类精度依赖于所有弱分类器。无论是应用于人造数据还是真实数据，Adaboost都能显著的提高学习精度。
3.Adaboost算法不需要预先知道弱分类器的错误率上限，且最后得到的强分类器的分类精度依赖于所有弱分类器的分类精度，可以深挖分类器的能力。Adaboost可以根据弱分类器的反馈，自适应地调整假定的错误率，执行的效率高。

缺点：
在Adaboost训练过程中，Adaboost会使得难于分类样本的权值呈指数增长，训练将会过于偏向这类困难的样本，导致Adaboost算法易受噪声干扰。此外，Adaboost依赖于弱分类器，而弱分类器的训练时间往往很长。对离散数据点敏感

参考链接：
【1】《机器学习实战》Peter Harrington(美) 人民邮电出版社
【2】[Machine Learning & Algorithm] 随机森林（Random Forest）
【3】机器学习实战之AdaBoost算法
【4】Adaboost原理详解

相关文章
-------------本文结束感谢您的阅读-------------